푸리에 변환 뽀개기 1

푸리에 변환은 공학과 과학의 거의 모든 분야에서 쓰이고 있습니다. 신호 처리, 이미지 처리, 회로 설계, 분광학, 결정학 등등 예시를 들자면 끝이 없죠. 제가 그랬듯이, 푸리에 변환을 쓰고는 있지만 이해하지 못한 채로 찝찝한 마음을 가지고 있기도 합니다. 하지만 모든 일이 그렇듯 푸리에 변환 역시 이해하고 나면 별 것 아닙니다. 최대한 간결하면서도 찝찝합이 남지 않도록 푸리에 변환을 이해해 보도록 하겠습니다.

이 글은 시리즈입니다. 첫번째 글은 푸리에 변환을 이해하기 위한 배경 지식을 다루고 있습니다.

이 글은 스탠포드 대학의 푸리에 변환과 응용 강의와 그 강의 노트를 요약한 글임을 먼저 밝힙니다.

복소수#

푸리에 변환을 이해하기 위해서는 몇가지 배경 지식이 필요합니다. 첫번째는 복소수(complex numbers)입니다. $$ i = \sqrt{-1} $$ 아마 고등학교에서 처음 복소수라는 것을 접하게 되었을 겁니다. 여기서는 두가지만 짚고 넘어가고자 합니다.

첫번째, 복소수를 쓰는 것은 우리가 앞으로 다룰 수식을 매우 단순하게 만들어 줍니다. 이게 복소수를 쓰는 유일한 이유는 아니지만, 좋은 이유죠.

두번째, 우리는 앞으로 실수인 어떤 대상(예를 들면 실수 신호)을 표현하기 위해 복소수를 쓸 것입니다. 이게 처음에는 이상해 보일 수도 있습니다. 어쩌면 실수와 허수의 관계에 대한 철학적인 고민에 빠질 수도 있습니다. 하지만 익숙해지는 것 외에는 별 방도가 없습니다. 허수와 실수가 어떻게 연결될 수 있는지는 오일러 공식을 다루며 살펴보겠습니다.

실수부와 허수부#

복소수는 두 개의 실수로 이루어집니다. 실수부(real part)와 허수부(imaginary part)입니다. $$ z = x + iy $$ x와 y는 실수이고, $ i^2 = -1 $ 입니다. x를 실수부, y를 허수부라고 부릅니다.

켤레복소수#

$z = x + iy$의 켤레복소수(complex conjugate)는 다음과 같습니다. $$ \overline{z} = x - iy $$ 켤레복소수에서는 다음 공식들이 성립합니다. $$ \overline{z + w} = \overline{z} + \overline{w} $$

$$ \overline{zw} = \overline{z} * \overline{w} $$

복소수의 크기#

$z = x + iy$의 크기(magnitude)는 다음과 같습니다. $$ | z | = \sqrt{x^2 + y^2} $$

극좌표 형식#

복소수가 두 개의 실수로 이루어지기 때문에, $z = x + iy$를 $(x, y)$ 쌍에 연결시키는 건 자연스러운 일입니다. 따라서 $z$를 데카르트 좌표계(Cartesian coordinates) 위의 한 점으로 표현할 수 있습니다. 이때 가로축은 “실수축(real axis)”, 세로축은 “허수축(imaginary axis)“이라고도 부릅니다.

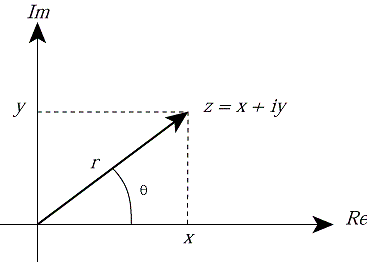
극좌표 $r$과 $\theta$를 도입해서 복소수 $z = x + iy$와 다음 식으로 연결시킬 수도 있습니다. $$ r = \sqrt{x^2 + y^2} $$

$$ \theta = \tan^{-1}(\frac{y}{x}) $$

$\theta$ 각도는 편각(argument) 또는 페이즈(phase)라고 불립니다.

극좌표에서 데카르트 좌표로 변환하면서 우리는 복소수의 극좌표 형식(polar form)을 얻게 됩니다. $$ x + iy = r\cos \theta + ir\sin \theta = r(\cos \theta + i\sin \theta) $$

복소지수와 오일러 공식#

복소지수#

앞으로 우리는 복소지수함수(complex exponential function)를 자주 보게 될 것입니다. 복소수 $z$에 대해서 지수 함수 $e^z$는 실수인 경우와 마찬가지로 테일러 급수(Tayor series)로 정의됩니다. 지수함수가 테일러 급수로 정의된다는 걸 알아둬서 나쁠 건 없겠죠. $$ e^z = 1 + z + \frac{z^2}{2!} + \frac{z^3}{3!} + \dots = \sum_{n=0}^{\infty}\frac{z^n}{n!} $$ 지수함수가 단지 복소수의 합, 곱, 상수배로 정의된다는 걸 알 수 있습니다. 따라서 켤레복소수에 대해 다음이 성립합니다. $$ \overline{e^z} = e^{\overline{z}} $$

오일러 공식#

복소지수함수에서 지수(exponent)가 순수한 허수일 때 재밌는 현상이 일어납니다. 바로 오일러 공식(Euler’s formula)라고 불리는 공식입니다. $$ e^{i\theta} = \cos\theta + i\sin\theta $$ 오일러 공식은 놀라운 발견입니다. 지수함수가 사인이나 코사인 같은 삼각함수와 관련이 있다니 누가 상상이나 해보았을까요?

$\theta = \pi$를 대입하면 다음을 얻게 됩니다. $$ e^{i\pi} + 1 = 0 $$ 이는 수학에서 가장 아름다운 공식으로 알려져 있습니다.

오일러 공식의 증명#

오일러 공식을 증명하는 방법은 여러가지가 있지만, 가장 간단하고 제가 제일 좋아하는 증명을 소개하겠습니다. 테일러 급수를 이용한 증명입니다. $$ \sin x = \sum^{\infty}_{n=0}\frac{(-1)^n}{(2n+1)!}x^{2n+1} = x - \frac{x^3}{3!} + \frac{x^5}{5!} + \dots $$

$$ \cos x = \sum^{\infty}_{n=0}\frac{(-1)^n}{(2n)!}x^{2n} = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} + \dots $$

$$ e^z = \sum_{n=0}^{\infty}\frac{z^n}{n!} = 1 + z + \frac{z^2}{2!} + \frac{z^3}{3!} + \dots $$

마지막 급수에서 $z = ix$로 대체하면 다음을 얻게 됩니다. $$ e^{ix} = 1 + ix + \frac{(ix)^2}{2!} + \frac{(ix)^3}{3!} + \dots $$

$$ = 1 + ix - \frac{x^2}{2!} - i\frac{x^3}{3!} + \frac{x^4}{4!} + i\frac{x^5}{5!} - \dots $$

$$ = (1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \dots ) + i(x - \frac{x^3}{3!} + \frac{x^5}{5!} - \dots) $$

$$ = \cos x + i\sin x $$

오일러 공식의 활용#

극좌표 형식 $z = r(\cos \theta + i \sin \theta)$은 이제 다음과 같이 쓸 수 있습니다. $$ z = re^{i\theta} $$ 여기서 $r = |z|$ 는 복소수의 크기이고 $\theta$는 복소수의 페이즈입니다.

오일러 공식을 이용하면 사인과 코사인의 합공식을 유도하는 것 정도는 식은 죽 먹기입니다. 복소지수함수를 두가지 방식으로 풀어 써 봅시다. 한편으로, $$ e^{i(\alpha + \beta)} = e^{i\alpha}e^{i\beta} $$

$$ = (\cos \alpha + i\sin \alpha)(\cos \beta + i\sin \beta) $$

$$ = (\cos \alpha \cos \beta - \sin \alpha \sin \beta) + i(\sin \alpha \cos \beta+ \cos \alpha \sin \beta) $$

다른 한편으로는, $$ e^{i(\alpha + \beta)} = \cos (\alpha + \beta) + i\sin (\alpha + \beta) $$ 실수부와 허수부를 각각 같다고 두면 다음을 얻습니다. $$ \cos (\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta $$

$$ \sin (\alpha + \beta) = \sin \alpha \cos \beta+ \cos \alpha \sin \beta $$

오일러 공식을 이용해 삼각함수의 합공식을 유도해본 이유는 이 유도 과정이 수학에서 아주 중요한 원칙 하나를 드러내주기 때문입니다.

같은 것을 두가지 다른 방식으로 풀어낼 수 있다면, 어쩌면 굉장히 의미 있는 일을 한 것이다.

어떤 면에서 이는 푸리에 변환의 정수입니다. 앞으로 보게 되겠지만 푸리에 변환은 같은 신호를 시간 도메인과 주파수 도메인 두가지 다른 시각으로 볼 수 있게 해주기 때문입니다. 때때로 이는 굉장히 의미 있는 일입니다.

오일러 공식의 활용 2#

지금까지 우리는 오일러 공식 $e^{i\theta} = \cos\theta + i\sin\theta$에 대해 살펴봤습니다. 알아둬서 나쁠 것 없는 공식이었죠. 이제 잠시 $\theta$를 $t$로 바꾸어 봅시다. $$ e^{it} = \cos t + i\sin t $$ 위 식이 평면에서 시간에 따라 움직이는 점을 나타낸다고 생각해 보죠. 이 점은 어떻게 움직이는 점일까요? 복소수의 극좌표 형식으로 보았을 때 크기 $r = 1$이기 때문에 이 점은 단위원(unit circle)을 따라 도는 점입니다. $t$가 $0$에서 $2\pi$까지 움직이며 시계 반대 방향으로 원을 딱 한번 돌지요.

위 식을 살짝 바꾼 다음 식을 다루는 게 좀 더 편리합니다. $$ e^{2\pi i t} = \cos 2\pi t + i\sin 2\pi t $$ 코사인과 사인에서 알 수 있듯이 위 식은 1Hz의 주파수를 갖습니다. $2\pi$가 있느냐 없느냐는 주파수를 Hz, 즉 초당 회전수 단위로 볼 것인가 각진동수(angular frequency), 즉 초당 라디안(radien) 으로 볼 것인가의 차이입니다. $2\pi$가 있으면 $t$가 0부터 1까지 가면서 점이 단위 원을 시계 반대 방향으로 한번 돌게 되죠. $e^{2\pi i t}$에 있는 단위는 다음과 같습니다. $$ e^{2\pi \text{ radians/cycle} * i * 1 \text{ cycles/sec} * t \text{ sec}} $$ $2\pi$가 없다면 $e^{it}$의 단위는 다음과 같습니다. $$ e^{i * 1 \text{ radians/sec} * t \text{ sec}} $$ 이제 우리는 신호의 크기(amplitude), 주파수, 페이즈 변화(phase shift)를 복소지수함수로 편하게 나타낼 수 있습니다. $$ Ae^{i(2\pi\textit{v} t + \phi)} $$ 이 신호의 크기는 $A$입니다. 즉 이 점은 반지름의 크기가 $A$인 원을 돌고 있는 것입니다. $\textit{v}$가 양수라고 가정하면 이 점은 시계 반대 방향으로 초당 $\textit{v}$번 원을 돌고 있습니다. 페이즈 $\phi$는 원에서 시작점의 각도을 나타냅니다.

$\textit{v}$가 음수면 어떻게 될까요? 간단하게 시계 반대 방향에서 시계 방향으로 움직임의 방향이 바뀐다고 생각하면 됩니다. 양의 주파수(positive frequency)는 시계 반대 방향을 뜻하고 음의 주파수(negative frequency)는 시계 방향을 뜻합니다.