Recurrent Neural Network (RNN) 이해하기

Recurrent Neural Network (RNN) 이해하기#

음악, 동영상, 에세이, 시, 소스 코드, 주가 차트. 이것들의 공통점은 무엇일까요? 바로 시퀀스라는 점입니다. 음악은 음계들의 시퀀스, 동영상은 이미지의 시퀀스, 에세이는 단어들의 시퀀스로 볼 수 있습니다. 시퀀스의 길이는 가변적입니다. 소설에는 한 페이지짜리 단편소설도 있고 열권짜리 장편소설도 있죠. 기존의 뉴럴 네트워크 알고리즘은 이미지처럼 고정된 크기의 입력을 다루는 데는 탁월하지만, 가변적인 크기의 데이터를 모델링하기에는 적합하지 않습니다.

RNN(Recurrent Neural Network, 순환신경망)은 시퀀스 데이터를 모델링 하기 위해 등장했습니다. RNN이 기존의 뉴럴 네트워크와 다른 점은 ‘기억’(다른 말로 hidden state)을 갖고 있다는 점입니다. 네트워크의 기억은 지금까지의 입력 데이터를 요약한 정보라고 볼 수 있습니다. 새로운 입력이 들어올때마다 네트워크는 자신의 기억을 조금씩 수정합니다. 결국 입력을 모두 처리하고 난 후 네트워크에게 남겨진 기억은 시퀀스 전체를 요약하는 정보가 됩니다. 이는 사람이 시퀀스를 처리하는 방식과 비슷합니다. 이 글을 읽을 때도 우리는 이전까지의 단어에 대한 기억을 바탕으로 새로운 단어를 이해합니다. 이 과정은 새로운 단어마다 계속해서 반복되기 때문에 RNN에는 Recurrent, 즉 순환적이라는 이름이 붙습니다. RNN은 이런 반복을 통해 아무리 긴 시퀀스라도 처리할 수 있는 것입니다.

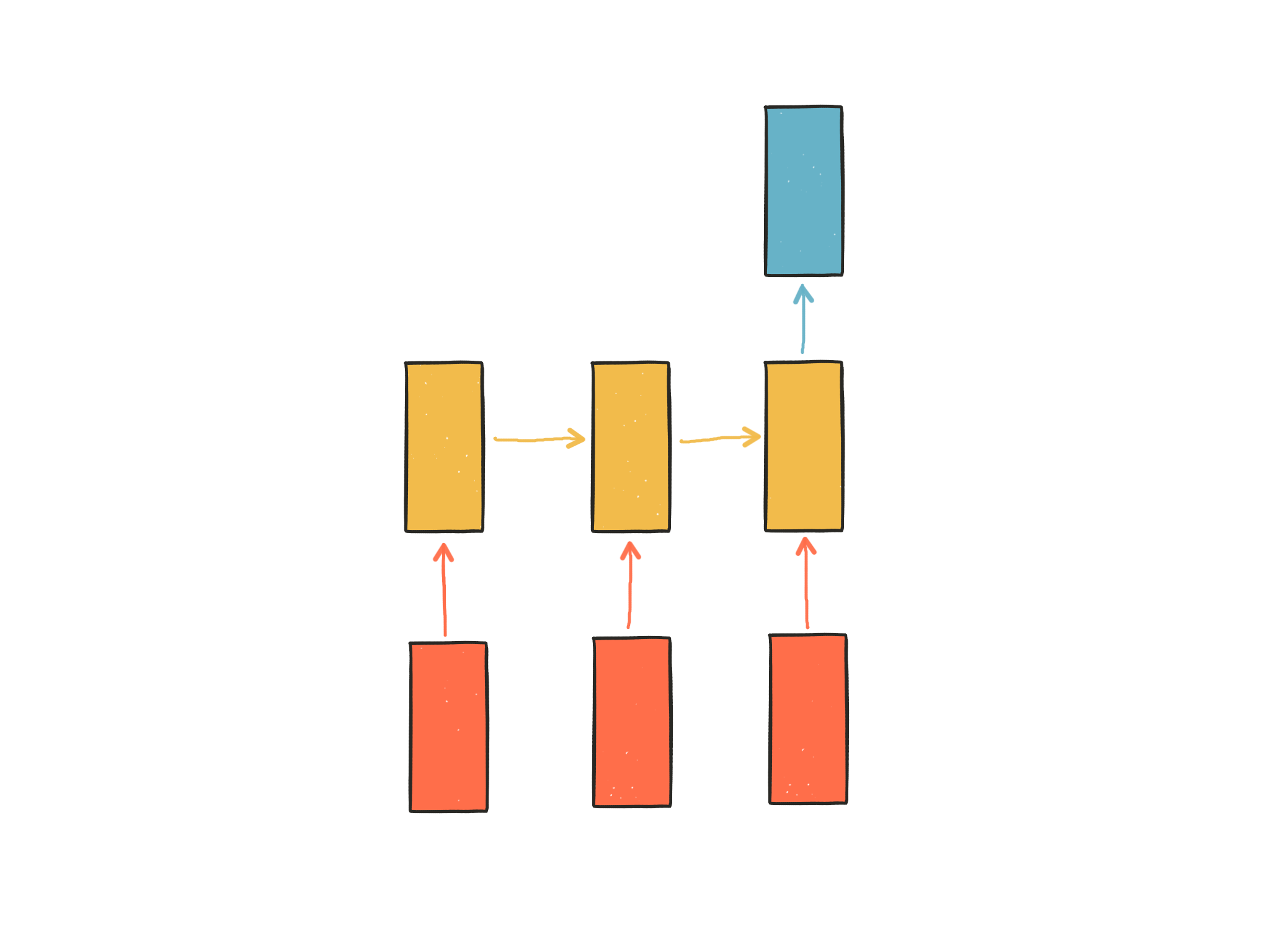
RNN 다이어그램

위 다이어그램에서 빨간색 사각형은 입력, 노란색 사각형은 기억, 파란색 사각형은 출력을 나타냅니다. 첫번째 입력이 들어오면 첫번째 기억이 만들어집니다. 두번째 입력이 들어오면 기존의 기억과 새로운 입력을 참고하여 새 기억을 만듭니다. 입력의 길이만큼 이 과정을 얼마든지 반복할 수 있습니다. 각각의 기억은 그때까지의 입력을 요약해서 갖고 있는 정보입니다. RNN은 이 요약된 정보를 바탕으로 출력을 만들어 냅니다.

What can RNNs do?#

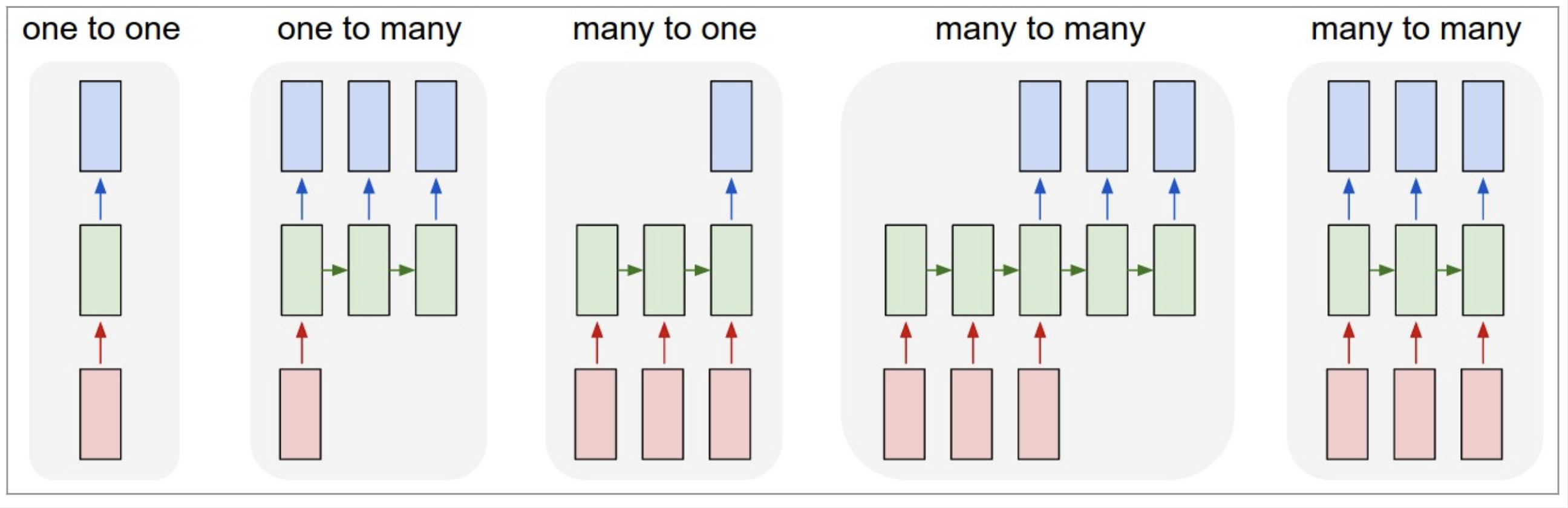
RNN의 입력과 출력은 우리가 네트워크에게 시키고 싶은 것이 무엇이냐에 따라 얼마든지 달라질 수 있습니다. 아래는 몇가지 예시입니다.

고정크기 입력 & 고정크기 출력. 순환적인 부분이 없기 때문에 RNN이 아닙니다.
고정크기 입력 & 시퀀스 출력. 예) 이미지를 입력해서 이미지에 대한 설명을 문장으로 출력하는 이미지 캡션 생성
시퀀스 입력 & 고정크기 출력. 예) 문장을 입력해서 긍부정 정도를 출력하는 감성 분석기
시퀀스 입력 & 시퀀스 출력. 예) 영어를 한국으로 번역하는 자동 번역기
동기화된 시퀀스 입력 & 시퀀스 출력. 예) 문장에서 다음에 나올 단어를 예측하는 언어 모델

이미지 캡션 생성#

이미지를 처리하는 CNN(Convolutional Neural Network)과 RNN을 결합하여 이미지를 텍스트로 설명해주는 모델을 만드는 것이 가능합니다. 이 모델은 위의 구조들 중 두번째, 고정크기 입력 & 시퀀스 출력에 해당합니다. 이미지라는 고정된 크기의 입력을 받아서 몇 단어로 표현될지 모를 가변적인 길이의 문장을 만들어내기 때문입니다.

이미지 캡션 생성

Show and Tell: A Neural Image Caption Generator

자동 번역#

구글의 번역기와 네이버의 파파고는 RNN을 응용한 모델로 만들어졌습니다. RNN 기반 모델은 기존 통계 기반 모델의 비해 우수한 성능을 낸다고 알려져 있습니다. 이 모델은 시퀀스 입력 & 시퀀스 출력 구조를 갖고 있습니다. 이 구조의 모델을 다른 말로 encoder-decoder 모델이라고도 부릅니다.

자동 번역

Google’s Neural Machine Translation System: Bridging the Gap between Human and Machine Translation

Show me the code#

Problem definition#

지금까지는 RNN에 대한 개념적인 설명이었습니다. 이제부터 수식과 코드를 통해서 RNN에 대해 구체적으로 살펴보겠습니다. 이해를 위해서 간단한 RNN 모델을 직접 구현해 보겠습니다. 뉴럴 네트워크 분야에서는 고전적인 문제인 MNIST 숫자 손글씨 맞추기를 RNN으로도 풀 수 있습니다. 물론 이미지 그 자체는 고정된 크기의 데이터지만, 약간의 트릭을 써서 시퀀스 데이터로 만들 수 있습니다.

이 모델에서는 MNIST의 28 * 28 크기의 이미지를 28차원 벡터로 이루어진 28개의 시퀀스로 보고 RNN에 입력합니다. 출력은 0부터 9까지의 숫자입니다. 이렇게 모델의 입력과 출력을 구성하고 과연 RNN이 숫자 분류기로서 어느 정도의 성능을 낼 수 있을지 실험해 보겠습니다.

Variable definition#

가장 먼저 할 일은 변수를 정의하는 것입니다. 아래 다이어그램은 만들려고 하는 모델을 변수 기호와 함께 나타낸 것입니다. $x_t$는 t 시간 스텝에서의 입력 벡터, $s_t$는 t 시간 스텝에서 RNN의 기억을 담당하는 hidden state, $o$는 출력 벡터입니다. U, W, V는 모델의 파라미터입니다. 첫 다이어그램에 없던 $s_{init}$은 hidden state의 초기값으로, 구현을 위해 필요한 부분입니다.

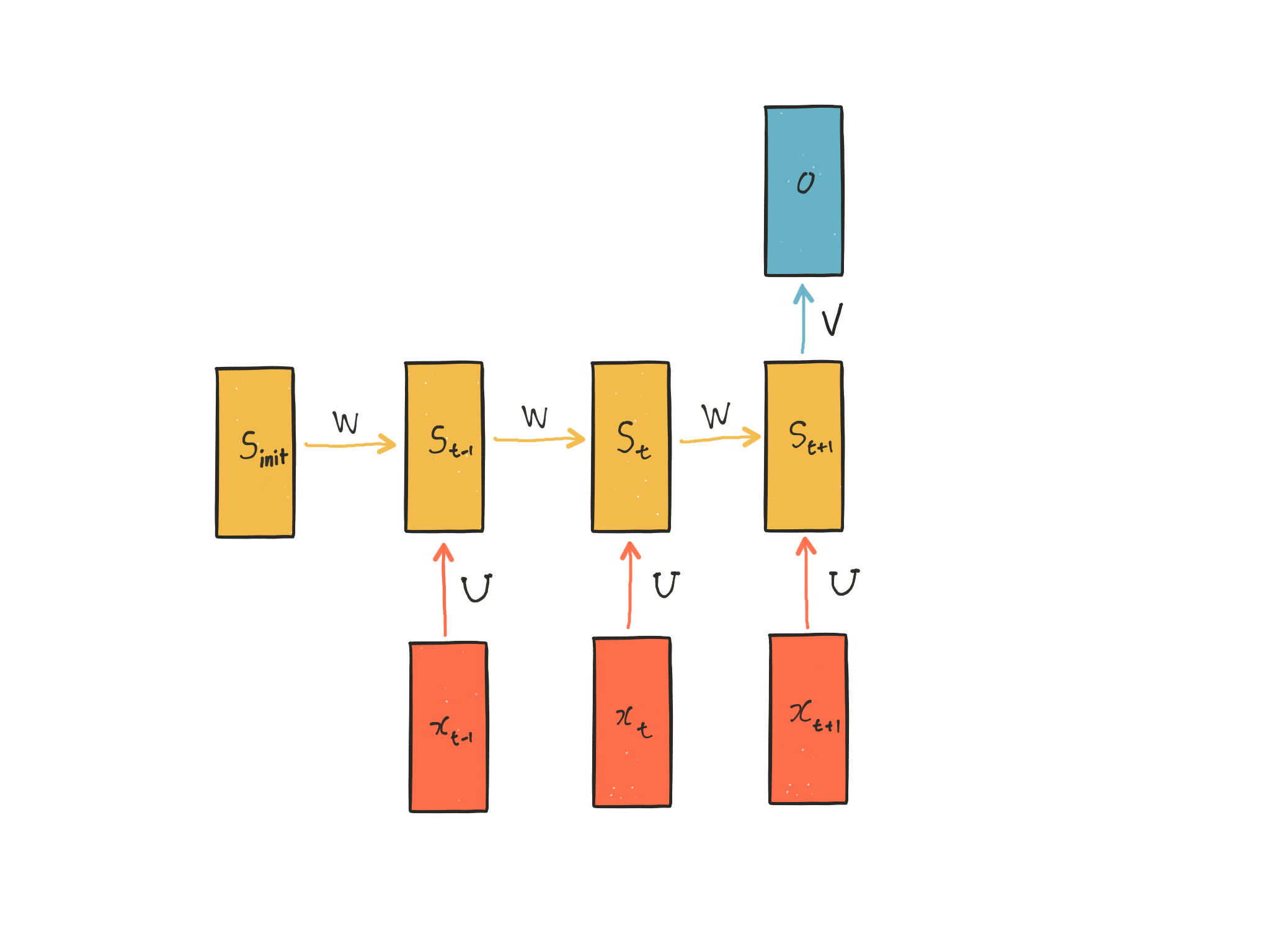
변수가 정의된 RNN 다이어그램

변수들의 차원을 써보면 이해하는 데 많은 도움이 됩니다.

$x_t \in \mathcal{R}^{28}$
$o \in \mathcal{R}^{10}$
$s_t \in \mathcal{R}^{100}$
$U \in \mathcal{R}^{28 \times 100}$
$W \in \mathcal{R}^{100 \times 100}$
$V \in \mathcal{R}^{100 \times 10}$

텐서플로어를 이용해 변수를 정의해 보겠습니다.

import tensorflow as tf

batch_size = 100
h_size = 28
w_size = 28
c_size = 1
hidden_size = 100

MNIST 이미지를 변형하여 벡터의 시퀀스로 만드는 부분입니다. x_raw는 28x28 크기의 MNIST 이미지이고, 이를 tf.split을 이용해서 28조각으로 자르면 28차원 벡터가 28개 나열되어 있는 시퀀스로 만들 수 있습니다.

x_raw = tf.placeholder(tf.float32, shape=[batch_size, h_size, w_size, c_size]) # [100, 28, 28, 1] 
x_split = tf.split(x_raw, h_size, axis=1) # [100, 28, 28, 1] -> list of [100, 1, 28, 1]

우리가 맞춰야 하는 0부터 9까지의 label을 y로 두겠습니다.

y = tf.placeholder(tf.float32, shape=[batch_size, 10])

이제 모델 정의에 필요한 변수들인 U, W, V 및 hidden state s를 정의합니다.

U = tf.Variable(tf.random_normal([w_size, hidden_size], stddev=0.01))
W = tf.Variable(tf.random_normal([hidden_size, hidden_size], stddev=0.01)) # always square
V = tf.Variable(tf.random_normal([hidden_size, 10], stddev=0.01))

s = {}
s_init = tf.random_normal(shape=[batch_size, hidden_size], stddev=0.01)
s[-1] = s_init

이제 변수 정의를 마쳤습니다. 이제 이 변수들을 이용해서 RNN 모델을 만들어봅시다.

Model specification#

네트워크의 기억에 해당하는 hidden state $s_t$는 입력 x와 과거의 기억 $s_{t-1}$을 조합하여 만들어집니다. 조합하는 방식은 파라미터 U와 W에 의해 결정됩니다. U는 새로운 입력이 새로운 기억에 영향을 미치는 정도를, W는 과거의 기억이 새로운 기억에 영향을 미치는 정도를 결정한다고 볼 수 있습니다. 비선형함수로는 tanh나 ReLU가 주로 사용됩니다. 여기에서는 tanh를 쓰겠습니다.

$$s_t = tanh(x_tU + s_{t−1}W)$$

for t, x_split in enumerate(x_split):
    x = tf.reshape(x_split, [batch_size, w_size]) # [100, 1, 28, 1] -> [100, 28]
    s[t] = tf.nn.tanh(tf.matmul(x, U) + tf.matmul(s[t-1], W))

출력, 즉 예측값은 마지막 hidden state $s_t$로부터 계산됩니다. $s_t$와 V를 곱하는데, 여기서 V는 hidden state와 출력을 연결시켜주며 출력 벡터의 크기를 맞춰주는 역할을 합니다. 마지막으로 출력을 확률값으로 변환하기 위해 softmax 함수를 적용합니다. softmax 함수는 모든 출력값을 0 ~ 1 사이로 변환하고, 출력값의 합이 1이 되도록 합니다.

$$o = softmax(s_tV)$$

o = tf.nn.softmax(tf.matmul(s[h_size-1], V))

모델의 비용함수는 맞춰야 하는 숫자 y와 모델의 출력인 o 사이의 cross entropy로 정해집니다.

cost = -tf.reduce_mean(tf.log(tf.reduce_sum(o*y, axis=1)))

Training#

아래 코드는 일반적인 뉴럴 네트워크를 학습시키는 방법과 동일합니다.

최적화 알고리즘으로는 Gradient Descent를 쓰고, 학습 속도는 0.1로 정하겠습니다.

learning_rate = 0.1
trainer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)

TensorFlow에서 실제 계산을 수행하기 위해서는 세션을 열어야 합니다. 여기서는 결과를 즉각적으로 확인하기 위해 interactive session을 열겠습니다. 세션을 연 후에는 모든 변수를 초기화시켜 줍니다.

sess = tf.InteractiveSession()
init = tf.global_variables_initializer()
init.run()

우리가 데이터셋으로 쓸 MNIST 데이터를 가져오는 코드입니다. 데이터가 컴퓨터에 있다면 가져오고, 만약 없다면 자동으로 인터넷에서 다운로드를 받습니다.

import tensorflow.examples.tutorials.mnist.input_data as input_data

mnist = input_data.read_data_sets("data/", one_hot=True, reshape=False)
trainimgs, trainlabels, testimgs, testlabels \
 = mnist.train.images, mnist.train.labels, mnist.test.images, mnist.test.labels 
ntrain, ntest, dim, nclasses \
 = trainimgs.shape[0], testimgs.shape[0], trainimgs.shape[1], trainlabels.shape[1]

모델을 평가하기 위해 평가용 데이터셋을 따로 떼놓겠습니다.

test_inputs = testimgs[:batch_size]
test_outputs = testlabels[:batch_size]

모델의 정확도를 계산하기 위한 함수입니다.

def accuracy(network, t):
    
    t_predict = tf.argmax(network, axis=1)
    t_actual = tf.argmax(t, axis=1)

    return tf.reduce_mean(tf.cast(tf.equal(t_predict, t_actual), tf.float32))

acc = accuracy(o, y)

실제로 학습이 수행되는 부분입니다. 여기서는 간단하게 20번만 학습을 시켜보겠습니다.

for _ in range(20):
    for i in range(trainlabels.shape[0]//batch_size):
        inputs = trainimgs[i*batch_size:batch_size*(1+i)]
        outputs = trainlabels[i*batch_size:batch_size*(1+i)]
        feed = {x_raw:inputs, y:outputs}
        trainer.run(feed)

이제 모델의 정확도를 평가해봅시다.

acc.eval({x_raw:test_inputs, y:test_outputs})

0.92000002

정확도 92%가 나왔습니다. 나쁘지 않은 성적입니다!

이 글에서는 이해가 목적이었기 때문에 가장 간단한 모델을 설계했지만, 모델의 입력과 출력에 Affine layer를 붙이는 등 모델을 변형하면 훨씬 더 높은 정확도를 얻을 수 있습니다. 직접 시도해보면 RNN에 대한 이해도를 더욱 높일 수 있을 것입니다.

sess.close()

Conclusion#

이 글에서 우리는 RNN의 개념과 응용 사례를 살펴보고 간단한 문제를 RNN을 구현하여 풀어보았습니다.

글을 마치기 전에 RNN의 변형 모델에 대해서 간단하게 언급하려고 합니다. RNN은 강력한 모델이지만 물론 단점도 존재합니다. 가장 큰 단점은 시퀀스 중 중요한 입력과 출력 단계 사이의 거리가 멀어질 수록 그 관계를 학습하기 어려워진다는 점입니다. 이는 RNN이 가장 최근의 입력을 가장 강하게 기억하기 때문입니다. 이 점을 극복하기 위해 RNN의 여러 변형 모델들이 제안되고 연구되고 있습니다. 대표적인 변형 모델로는 LSTM이 있습니다. 또한 주의(attention) 기반 모델도 RNN의 단점을 극복하고 놀라운 성과를 내고 있습니다. RNN을 이해했다면 이러한 변형 모델들을 알아보는 것도 흥미로울 것입니다.